Dersom du synes grunnleggende algebra er vanskelig, så anbefaler jeg deg å ta en titt på dette først. Du finner innlegget om enkel bokstavregning her.
I algebra har vi noe som heter kvadratsetningene. Dette er 3 setninger som beskriver sammenhenger som ofte kommer til nytte i algebraisk arbeid. La oss ta en titt på hver av dem, og la oss gjøre noen øvningsoppgaver.
1.kvadratsetning
![]()
Hvorfor kalles dette en kvadratsetning? Jo fordi den beskriver arealet av et kvadrat, der hver side av kvadratet er (a+b) lang. Denne kan vi benytte oss av for å gjennomføre utregninger raskere:![]()
![]()
![]()
Se på definisjonen av 1.kvadratsetning, og se hvordan dette henger sammen. Når du ser sammenhengen, så kan du prøve deg på disse:![]()
![]()
![]()
Men dette er ikke alt. Det viktigste er faktisk at vi kan gå andre veien. Vi kan faktorisere enkelte uttrykk også:![]()
![]()
![]()
Ser du sammenhengen? Når du gjør det, så kan du prøve selv, ved å faktorisere disse uttrykkene:![]()
![]()
![]()
2.kvadratsetning
![]()
Hvorfor kalles dette en kvadratsetning? Igjen, fordi den beskriver arealet av et kvadrat, der hver side av kvadratet nå er (a-b) lang. Også her kan vi benytte dette for å gjennomføre utregninger raskere:![]()
![]()
![]()
Se på definisjonen av 2.kvadratsetning, og se hvordan dette henger sammen. Når du ser sammenhengen, så kan du prøve deg på disse:![]()
![]()
![]()
Men dette er ikke alt. Det viktigste er faktisk at vi kan gå andre veien. Vi kan faktorisere enkelte uttrykk også:![]()
![]()
![]()
Ser du sammenhengen? Når du gjør det, så kan du prøve selv, ved å faktorisere disse uttrykkene:![]()
![]()
![]()
Konjungatsetningen
![]()
Stemmer! Denne heter ikke “3.kvadratsetning”, og forklaringen er ganske innlysende. Den beskriver ikke noe kvadrat. Det er ikke en størrelse ganget med seg selv. Men, den likner på kvadratsetningene, og derfor vil mange kalle den for “den 3. kvadratsetning”.
Som med kvadratsetningene, så kan vi også bruke denne til å gjøre algebraiske operasjoner raskt:![]()
![]()
![]()
Også her kan vi jobbe motsatt vei; vi kan faktorisere uttrykk som passer inn i konjungatsetningen. Dersom et uttrykk er differansen mellom to kvadrater, så kan den faktoriseres:![]()
![]()
![]()
Var ikke den siste litt artig? Ikke det? OK….
La oss trene med noen øvningsoppgaver!
Regn ut!
Faktoriser uttrykkene!
…og hvis dette gikk greit, så kan du vel prøve deg på disse også.
Forenkle uttrykkene!
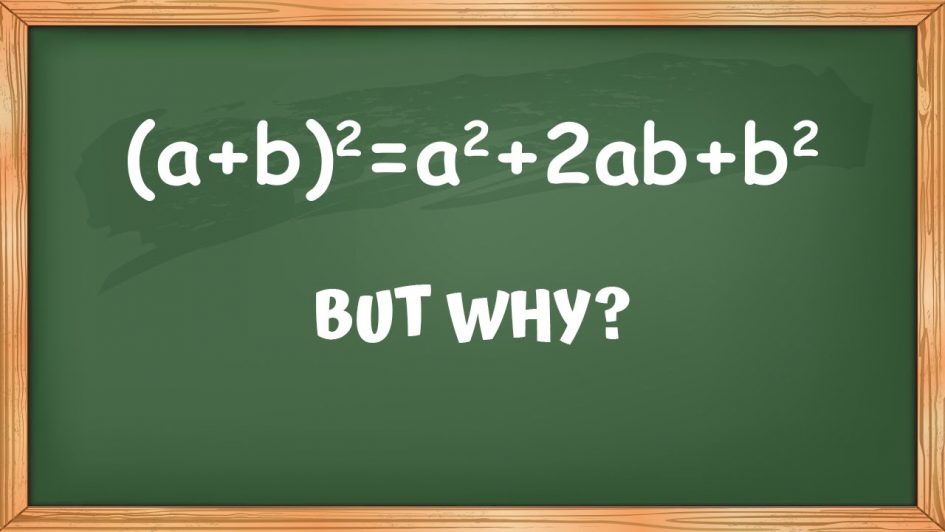
Recent Comments