Prinsippet med en likning er at begge sider av “=”-tegnet har lik verdi. Det er derfor det kalles en likning. Vi kunne sikkert kalt det en liknelse, men det ordet er liksom litt opptatt. Din oppgave er å finne ut hvilken verdi den ukjente har, som gjør at begge sider er like. F eks denne likningen:![]()
Din oppgave er å finne verdien av x, som gjør at 2x+1 har samme verdi som x+7. Det er bare ett riktig svar, og det er at x=6. Venstre side får da verdien 13 (2*6+1) og høyre side får verdien 13 (6+7). Siden 13=13, så har vi løst likningen riktig. La oss se på metoden.
Først og fremst; når vi jobber med likninger så behandler vi alltid begge sider likt. Det vi gjør på venstre side av “=”-tegnet, må vi også gjøre på høyre side. Målet vårt er å få en x alene på en side, og et tall på den andre siden. Under ser du likningen, og hvordan jeg tenker når jeg løser den
| Hvilken side er det flest x’er? Venstre! Da kvitter jeg meg med x’en på høyre side, altså trekker fra en x på begge sider. | |
| Mellomregning! Dette skriver jeg vanligvis ikke! | |
| Dette ser bedre ut, men jeg ville jo ha x’en alene på en side. Da fjerner jeg 1’tallet ved å trekke fra 1 på begge sider | |
| Mellomregning! Dette skriver jeg vanlivis ikke! | |
| Sånn! Da er jeg jo ferdig! |
Hvis du hang med på denne, så kan du vel løse et par likninger på egen hånd.
Finn x!
![]()
![]() PS! Motsatt av minus 1 er pluss 1.
PS! Motsatt av minus 1 er pluss 1.
Da har vi sett på enkle likninger. Hva skjer dersom vi begynner å blande inn brøker i likningen? Vel, vi kan fortsatt behandle begge sider likt, og siden brøk er det samme som å dele på noe, så kan vi faktisk bare gange begge sider av likningen. Se på dette eksemplet:![]()
Her har vi en brøk, der nevneren er 3. Det betyr at x skal deles på 3. Det motsatte av å dele er å gange, så derfor velger jeg å gange begge sider med 3. Når jeg ganger en side med 3, så er det viktig å utføre gangingen med alle ledd. Se her:
| Jeg ganger begge sider med 3. Legg merke til at alle ledd må ganges med 3. | |
| Hvilken side er det flest x’er? Høyre! Da tar jeg bort en x på hver side, slik at venstre side ikke lenger har x’er. | |
| Jeg vil ha x’ene alene, så jeg legger til 12 på begge sider, slik at 3x står igjen alene på høyre side. | |
| Nå vet jeg hva 2 x’er er. Hvis jeg nå deler på 2 på begge sider, så vet jeg hva en x er. | |
| Altså; x er 9. Prøv å sett det inn i den opprinnelige likningen, og se at det stemmer! |
Hang du med? Da synes jeg du bør prøve å løse disse likingene:
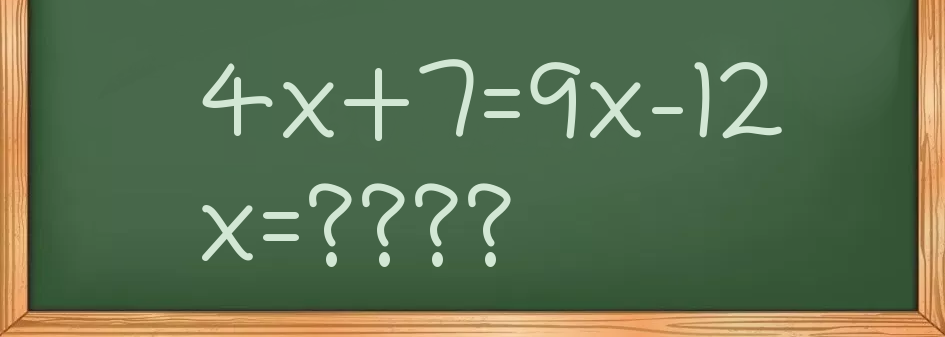
Recent Comments