Standardform er en måte å skrive veldig store eller veldig små tall på en måte som er lettere å lese og lettere å regne med. Systemet er rett og slett bare bygd opp rundt tierpotenser. Disse lønner det seg å kunne:
![]() – 1000 – ett tusen
– 1000 – ett tusen![]() – 1 000 000 – en million
– 1 000 000 – en million![]() – 1 000 000 000 – en milliard
– 1 000 000 000 – en milliard![]() – 1 000 000 000 000 – en billion
– 1 000 000 000 000 – en billion![]() – 1 000 000 000 000 000 – en billiard
– 1 000 000 000 000 000 – en billiard![]() – 0,001 – en tusendel
– 0,001 – en tusendel![]() – 0,000 001 – en milliondel
– 0,000 001 – en milliondel![]() – 0,000 000 001 – en milliarddel
– 0,000 000 001 – en milliarddel
Som du ser, så blir det fort et tøysete antall nuller i tallene, og de blir vanskelige å lese.
Eks 1
Utenlandsgjelden i usa er på 20 162 176 797 904 dollar. Dette tallet er vanskelig å lese, og de 9 siste sifrene er relativt uvesentlig i de fleste sammenhenger. Da er det enklere dersom tallet hadde blitt oppgitt på standardform:
Vi kunne skrevet, altså ca 20 billioner, som ville vært riktig matematisk, men det er ikke standardform. For at det skal være på standardform så må den første faktoren være mellom 1 og 10, og den andre faktoren en tierpotens. Korrekt standardform blir derfor:
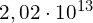
Eks2
Antall atomer i universet er stort. Man har kommet frem til en omtrentlig verdi, nemlig:100 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Denne verdien er omtrent umulig å lese, men på standardform ser det slik ut:
Altså, et ett-tall med 80 nuller bak…

Recent Comments