Metode
Et tall er enten et primtall, eller et produkt av primtall (sammensatt). Du husker sikkert at produkt er resultatet av et gangestykke :-). Tallet 11 er et primtall fordi vi ikke kan gange sammen tall og få 11. La oss se på tallene mellom 10 og 20.
- 11 – primtall
- 12 = 2*2*3 – produkt av primtall (jeg skriver ikke 4*3, fordi 4 også er produkt av primtall)
- 13 – primtall
- 14 = 2*7 – produkt av primtall
- 15 = 3*5 – produkt av primtall
- 16 = 2*2*2*2 – produkt av primtall
- 17 – primtall
- 18 = 2*3*3 – produkt av primtall
- 19 – primtall
- 20 = 2*2*5 – produkt av primtall
Her har jeg primtallfaktorisert 12, 14, 15, 16, 18 og 20. De andre tallene kan ikke faktoriseres, fordi de er primtall.
Metode for primtallfaktorisering
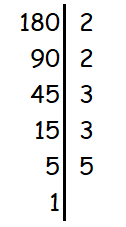
Her skal jeg primtallfaktorisere tallet 180. Jeg starter alltid med å skrive opp tallet, og tegner en loddrett strek ned på høyre side. Deretter starter jeg med det laveste primtallet (2) og spør meg selv: “Kan 180 deles på 2? Ja, og det blir 90.” Da skriver jeg 2 på høyre side av streken, og 90 under 180. Så fortsetter jeg. “Kan 90 deles på 2? Ja, og det blir 45.” Jeg skriver igjen 2 under det forrige 2-tallet, og 45 skriver jeg under 90. Så spør jeg: “Kan 45 deles på 2? Nei.” Da må jeg gå til det neste primtallet. “Kan 45 deles på 3? Ja, og det blir 15.” Jeg skriver 3 under 2-tallene, og 15 under 45. “Kan 15 deles på 3? Ja, og det blir 5.” Jeg skriver nok et 3-tall under 3 og skriver 5 under 15. “Kan 5 deles på 3? Nei! Kan 5 deles på 5? Ja, og det blir 1.” Jeg skriver 5 under 3-tallet, og 1 under 5. Nå er jeg ferdig. Resultatet mitt er: 180=2*2*3*3*5. Hvordan føringen ser ut, ser du på høyre side.
Hang du med? La oss prøve med et par øvningsoppgaver.
Faktoriser disse tallene!

Recent Comments