Fasit

Oppgave 1

Til skoleavslutningen blir det kjøpt inn 12 poser med smågodt. Tilsammen koster dette 312 kroner.

a)
Hvor mye koster det for en pose?

b)
Hver pose inneholder 450 gram. Hvor mange kilo blir det til sammen?

Oppgave 2

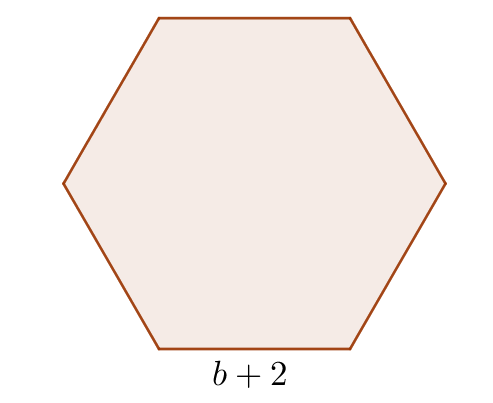
Figuren viser en regulær sekskant, der sidene er (b+2) lange. Lag et uttrykk for omkretsen av figuren.

Oppgave 3

Gudrun blander saft og heller det over i 6 saftmugger. Hun laget tilsammen 9 L ferdig blandet saft.

a)
Hvor mye saft er det i hver mugge?

Saften blandes i forholdet 1:5

b)
Hvor mye konsentrert saft er det i 3 L ferdig blandet saft?

Oppgave 4

Niclas har 240 km å kjøre for å komme på hytta, og han kjører med en gjennomsnittsfart på 80 km/h.

Hvor lang tid bruker han for å kjøre opp på hytta?

Oppgave 5

12\cdot 5\cdot 3=9\cdot 4 \cdot x

Hva er verdien av x?

Oppgave 6

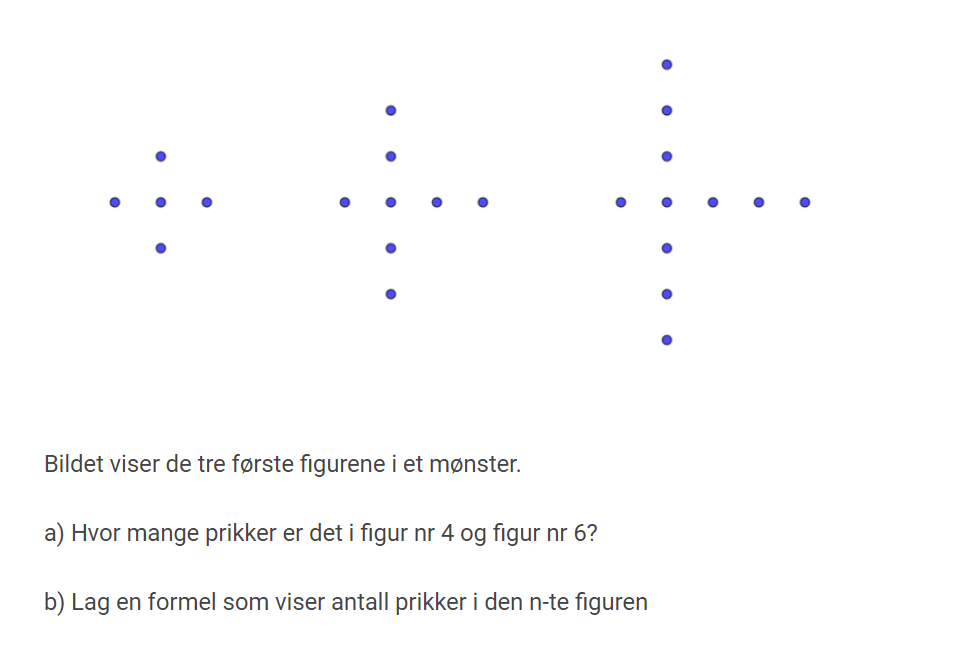
Oppgave 7

Fire venner teller pengene sine.

De har:

  • Niclas: 127 kr
  • Petter: 115 kr
  • Busch: 115 kr
  • Haaland: 237 kr

a) Hva er gjennomsnittsbeløpet til de fire vennene?

b) Hva er medianen?

Oppgave 8

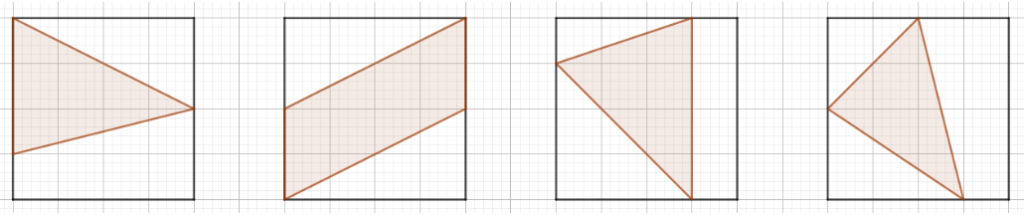
Regn ut areal og omkrets av figurene over.

** litt hjelp til kvadratrot ved Pytagoras når dere skal fine omkrets av figurene:

Oppgave 9

Arealet av sirkelen er 153 cm^2

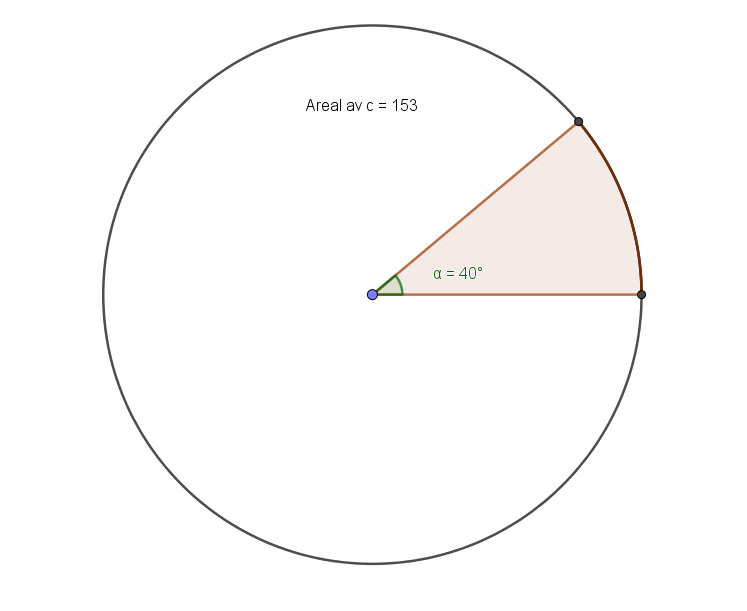
a) Hva blir arealet av sirkelsektoren?

En annen sirkel har også en sirkelsektor på 40 grader, men her er diameteren 20 cm.

b) Hva blir omkretsen av en slik sirkelsektor?

Oppgave 10

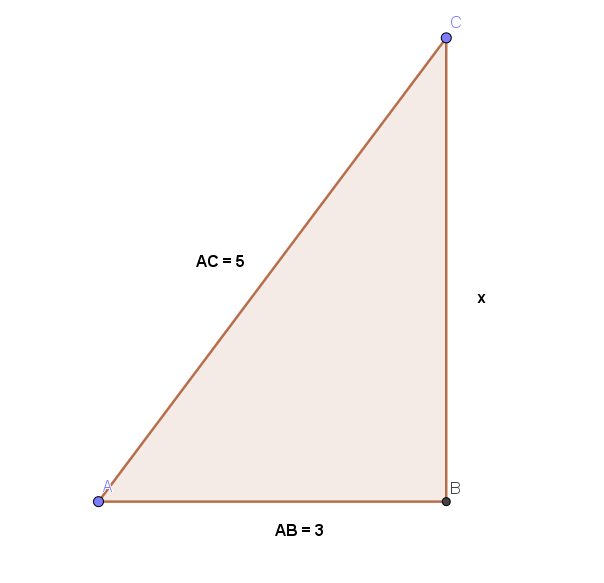
Hvor lang er siden x i den rettvinklede trekanten? (vis med Pytagoras).

Oppgave 11

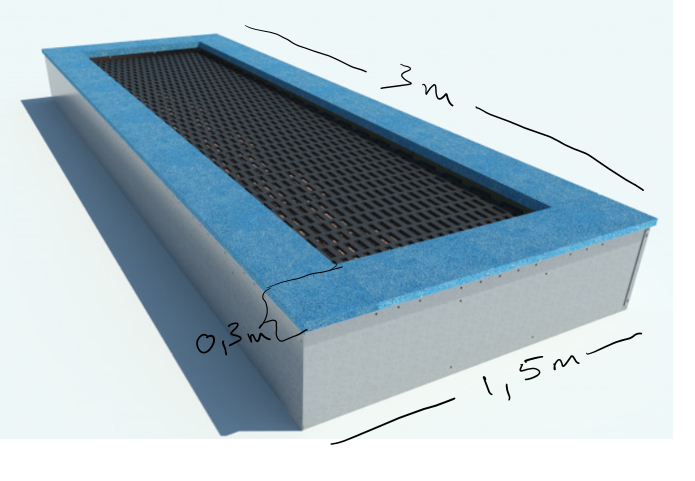
En trampoline er 3 m lang , 1,5m bred og har en kant(blå) som er 0,3m tykk.

a) Hva blir arealet av hele toppen av trampolinen?

b) Hva blir arealet av området man kan hoppe på (det svarte området)?

c) Hva blir arealet av området som den blå kanten dekker?

Oppgave 12

a) \frac{3}{6}\cdot 8

b) 6:\frac{1}{6}

Oppgave 13

a) 6b\cdot6b^2

b) \frac{36y^2+6y}{6y}

Oppgave 14

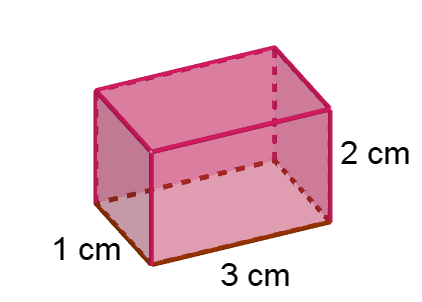
a) Regn ut volum og overflaten til kuben

b) Forklar hva som skjer med volumet dersom sidelengdene blir tre ganger så lange.

Oppgave 15

Løs likningene.

a) 4x-12=2x-2

b) 7+x=\frac{5x}{2}+1

Oppgave 16

I en pose ligger det 5 svarte og 3 gule kuler.

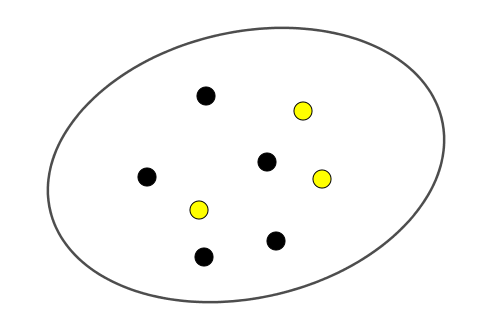
a) Hva er sannsynligheten for å tilfeldig trekke en gul kule?

b) Hva er sannsynligheten for tilfeldig å trekke to svarte kuler etter hverandre når den første kulen ikke blir lagt tilbake?

Oppgave 17

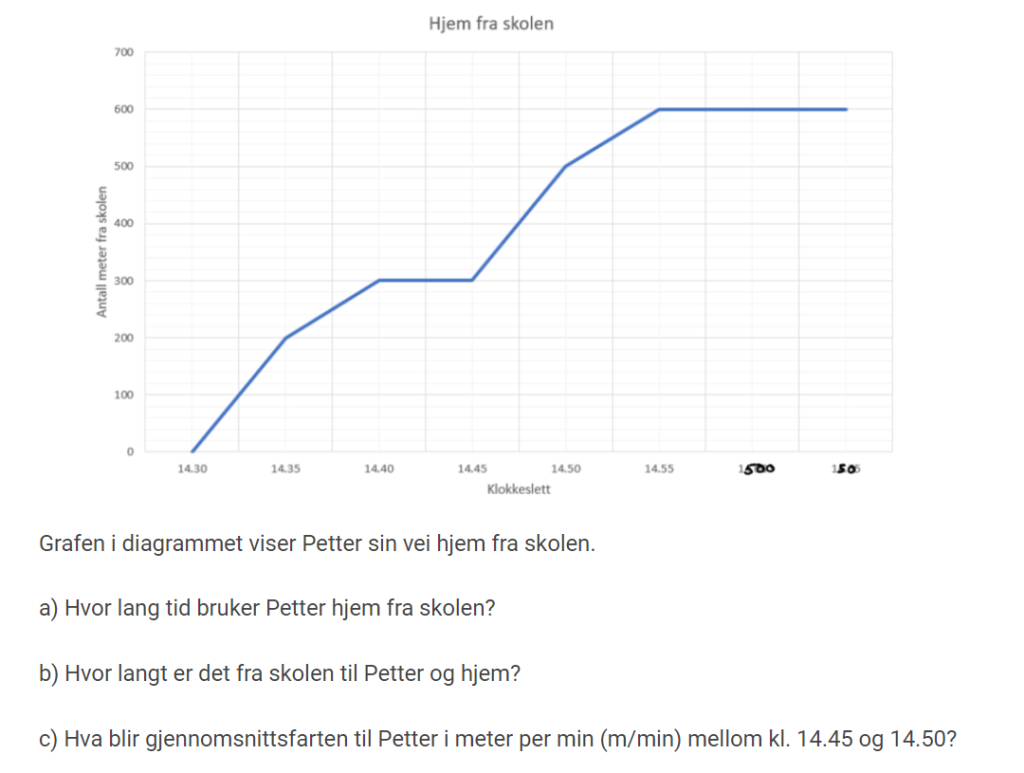
Oppgavene herfra er som Del2-oppgaver å regne. Det betyr at du kan benytte alle hjelpemidler, og presentere svar, fremgangsmåte og andre refleksjoner digitalt.

Oppgave 18

Personalrommet på verket skole har salg på pølser og kaffe. Tilbudet er “Ta 4 betal for 3”. (Du får den billigste gratis).

  • Prisen for pølse er 15 kr.
  • Prisen for en kaffe er 10 kr.

a) Gjør ferdig det påbegynte regnearket over hva de fire personene skal betale.

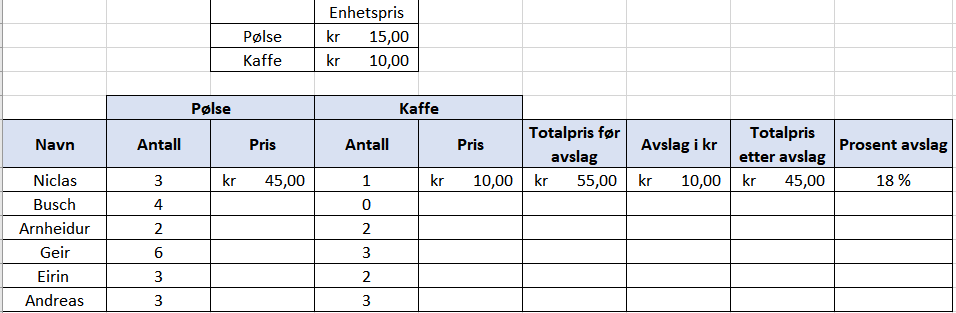
b) Finn ut hvor mange prosent hver av de 6 personene fikk i avslag.

c) Forklar hvorfor de maksimalt kan få 25% avslag.

Oppgave 19

Vi tenker oss at månen har form som en kule med en radius på ca 1737 km, og at månen dekkes av tre satellitter. Trekanten som satellittene danner tangerer sirkelen som månen danner. Vi kan tenke at månen bruker ca 24 timer på en rotasjon rundt seg selv.

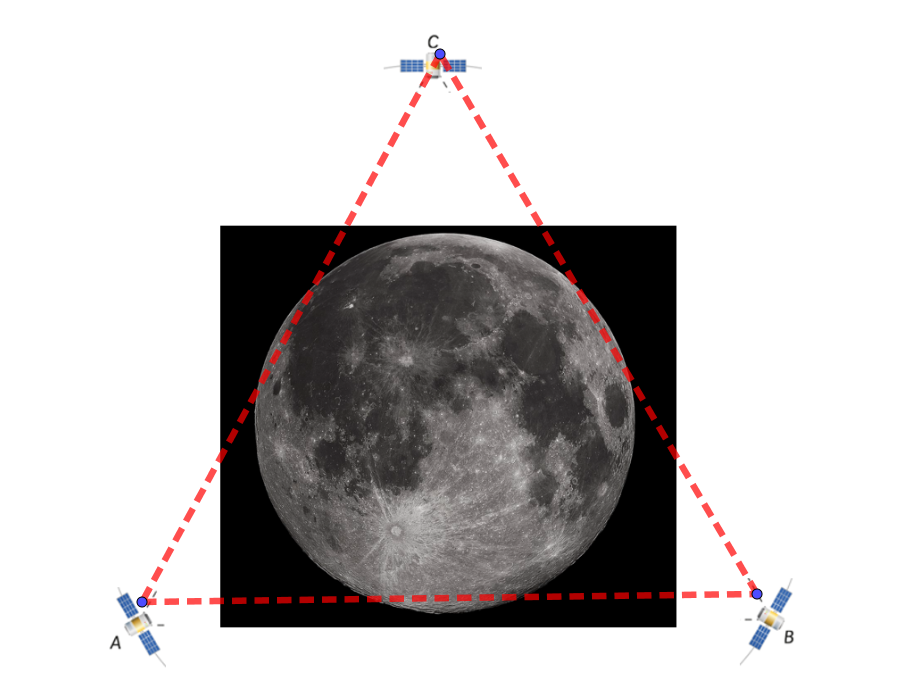
a) Hva blir arealet av overflaten til månen? (Overflate kule: 4\pi r^2)

b) Hva blir månens omkrets ved sentrum?

c) Vis ved regning at månens rotasjonshastighet (ved ekvator) er ca 455 km/t

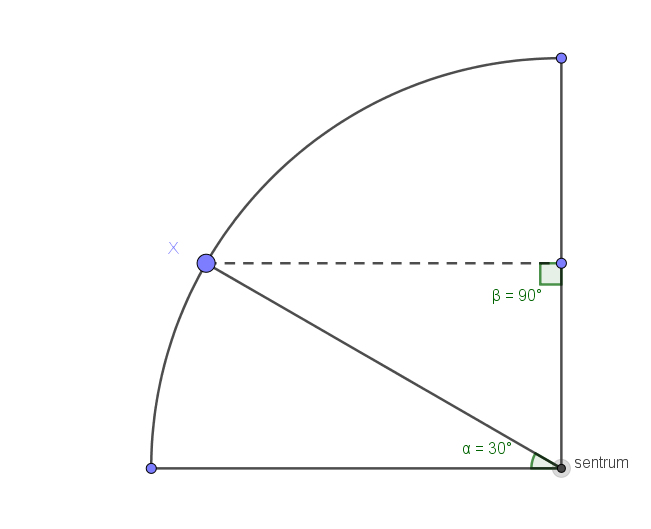
d) Hva blir månens rotasjonshastighet ved punkt X?

e) Hva blir omkretsen av den likesidete trekanten ABC som satellittene danner?

Oppgave 20

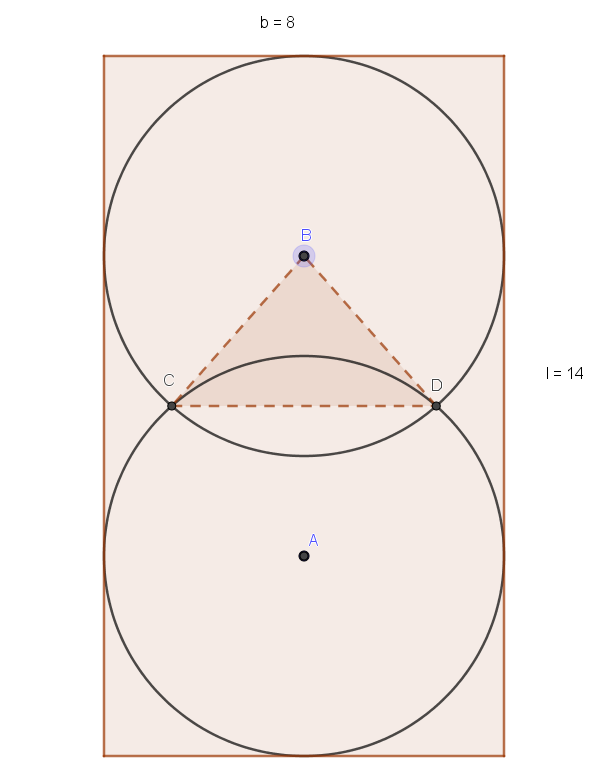
a) Forklar hvorfor avstanden AB = 6

b) Finn arealet av trekant BCD.

Oppgave 21

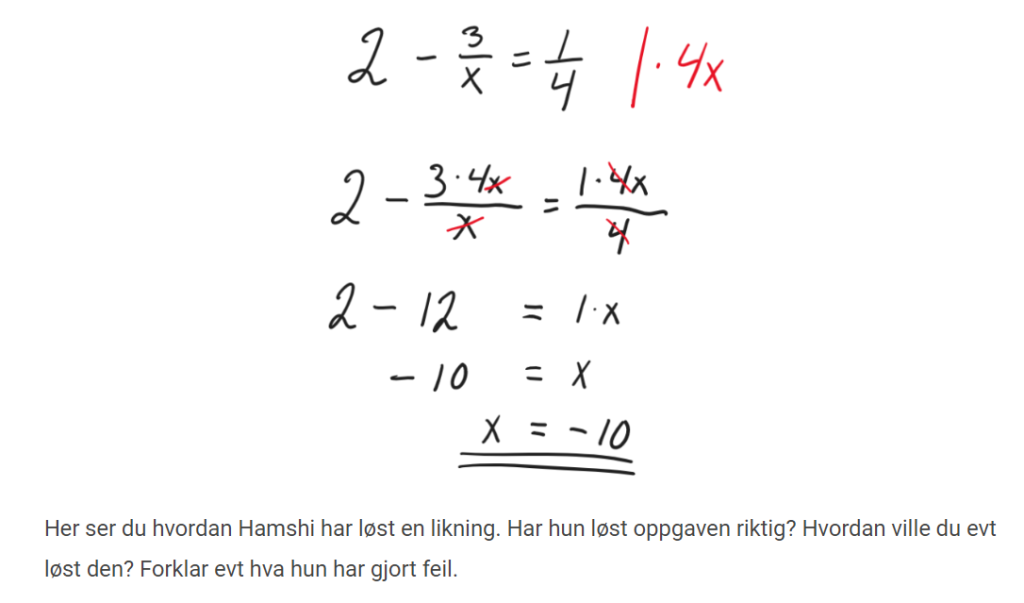
Oppgave 22

a) Lag ferdig et Excel-ark som viser utfallsrommet ved multiplikasjon av to terninger.

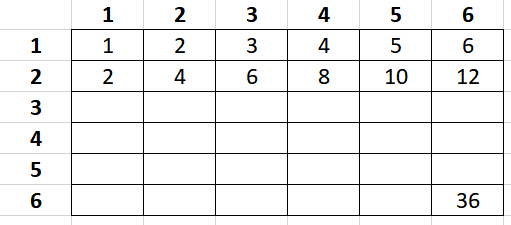
b) Bruk Excel-arket til å finne sannsynligheten for å få et produkt større enn 18 ved multiplikasjon av to terninger.

c) Lag en kode i Python og vis sannsynligheten for å få produkt 36 ved multiplikasjon av to terninger.