Fasit

Oppgave 1

a) 34 * 240

b) 844 : 4

Oppgave 2

a)

Ammar skal bake kake til klassen. I oppskriften står det at han trenger 200 gram mel i en kake til 4 personer. Hvor mye mel vil han trenge i en kake til 12 personer?

b)

En boks inneholder 450 gram mel. Hvor mange kilogram(kg) mel er det i 14 slike bokser?

Oppgave 3

Ammar kjøper 10 kg mel og betaler til sammen kr 230. Hvor mye koster en kg mel?

Oppgave 4

a) 0,5 \cdot \frac{2}{4}

b) 20:\frac{1}{5}

Oppgave 5

Forklar hvilken brøk som har størst verdi: \frac{10}{24} og \frac{5}{12}

Oppgave 6

Hvilken verdi har x?

4*6*5 = 4*10*x

Oppgave 7

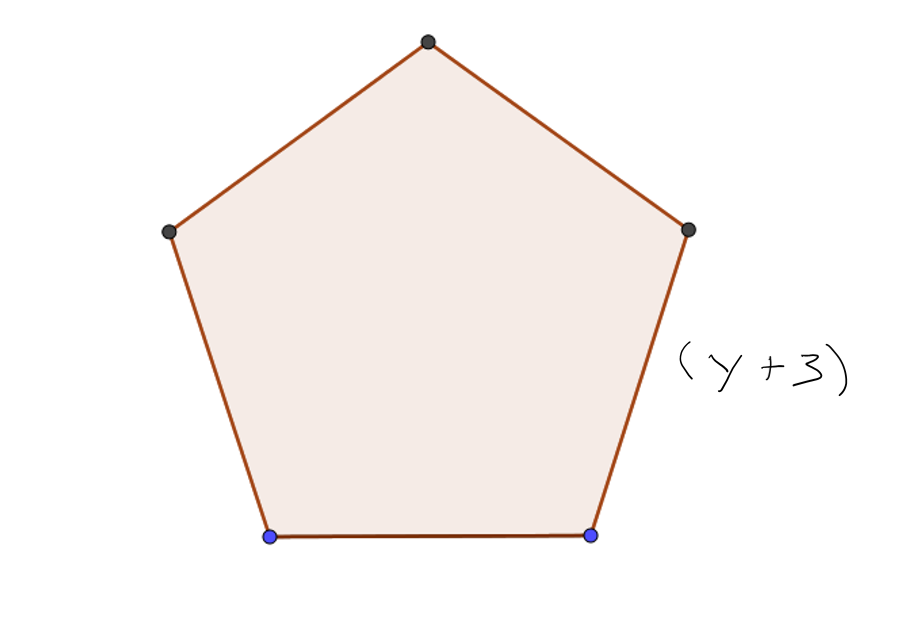
I noen poser ligger det 80 epler.

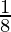  • \frac{1}{8} av eplene er grønne
  • 40 % av eplene er røde.
  • Resten av eplene er gule

a) Hvor mange gule epler ligger det i posen?

b) Hvor stor andel av eplene er gule?

(svaralternativer)
\frac{1}{2} – \frac{19}{40} – \frac{5}{12} – \frac{1}{3}

Oppgave 8

Regn ut og skriv svaret så enkelt som mulig.

a) 4y \cdot 6 \6y^2

b) \frac{25xy^2}{5xy}

c) \frac{4y(y+3)}{4y}

Oppgave 9

Finn en formel for omkretsen av den regulære femkanten når sidene er (y+3) lange.

Oppgave 10

Løs likningene.

a) x -9 = 17

b) 3x + 5 = x + 13

c) 5 + 2x = 5x -7

Oppgave 11

Niclas sykler med gjennomsnittsfart på 24 km/t. Hvor lang sykler han på 20 min

Oppgave 12

En butikk har salg og gir 30% rabatt på alle varer.

a) Du kjøper tre ulike varer med 30% rabatt. Hvor mange prosent rabatt får du til sammen?

b) Hvor mange kroner får du i rabatt når full pris på en vare er 650 kr?

c) Full pris på en vare er 4600 kr. Hvor mye koster varen på salg når det gis 30% i rabatt?

d) I en annen butikk det også salg. En vare som koster 1000 kr til full pris koster nå kr 750 kr. Hvor mange prosent rabatt gir butikken?

Oppgave 13

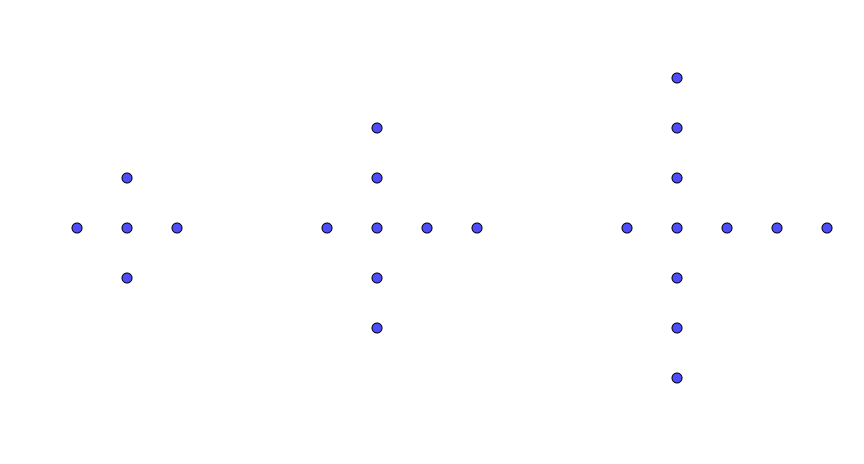
Bildet viser de tre første figurene i et mønster.

a) Hvor mange prikker er det i figur nr 4 og figur nr 6?

b) Lag en formel som viser antall prikker i den n-te figuren

Oppgave 14

a) Finn koordinatene til punktene i koordinatsystemet.

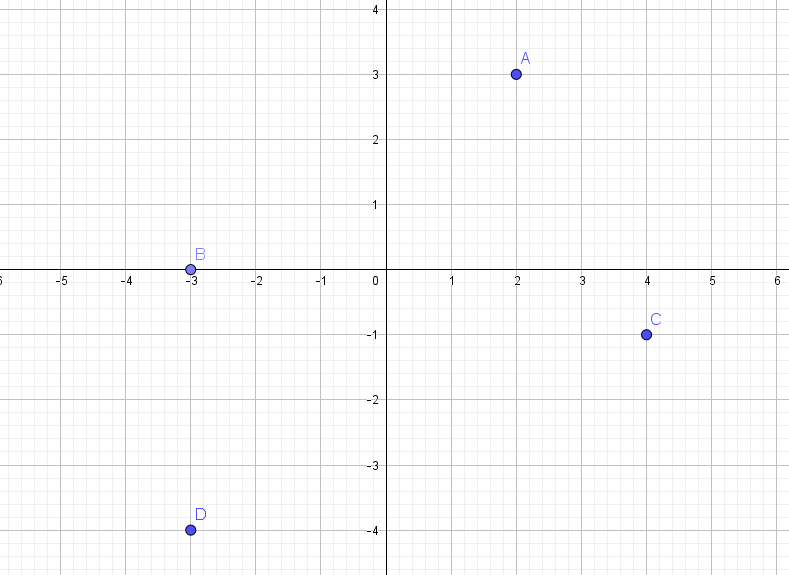
A:

B:

C:

D:

b) Tegn grafen til funksjonen f(x) = 3x-3 i koordinatsystemet

Oppgave 15

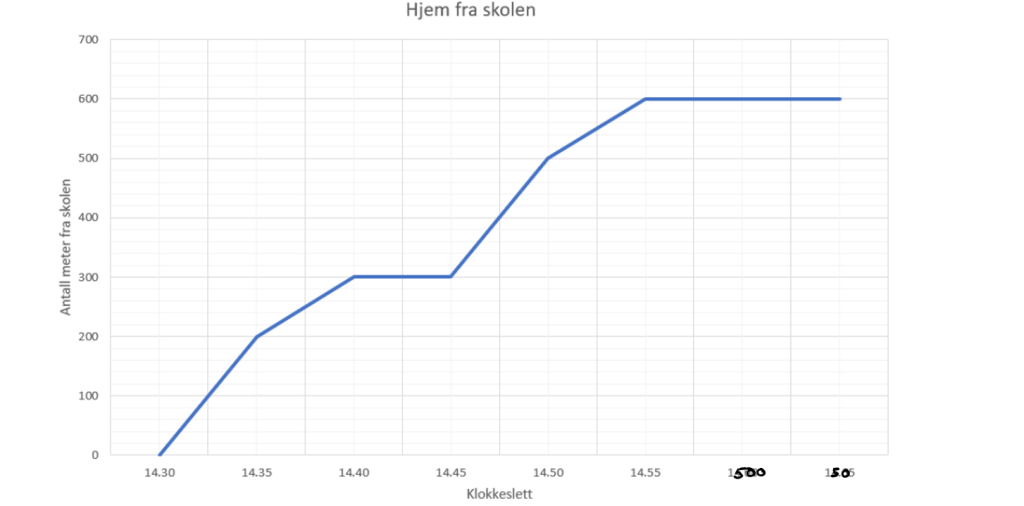
Grafen i diagrammet viser Petter sin vei hjem fra skolen.

a) Hvor lang tid bruker Petter hjem fra skolen?

b) Hvor langt er det fra skolen til Petter og hjem?

c) Hva blir gjennomsnittsfarten til Petter i meter per min (m/min) mellom kl. 14.45 og 14.50?

Oppgavene herfra er som Del2-oppgaver å regne. Det betyr at du kan benytte alle hjelpemidler, og presentere svar, fremgangsmåte og andre refleksjoner digitalt.

Oppgave 16

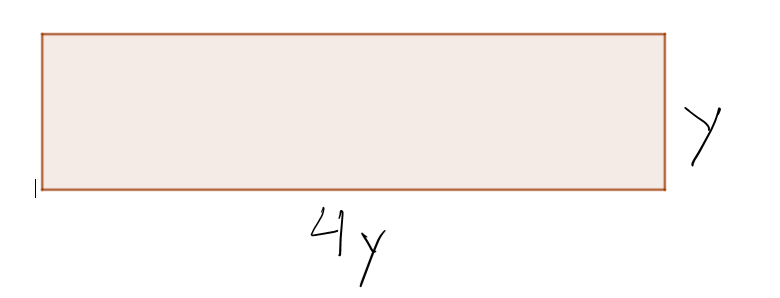
Omkrets: 2(l+b)
Areal: l*b

a) Hva blir formelen for omkrets og areal av rektangelet uttrykt med y?

b) Lag en likning og finn lengden av y hvis omkretsen av rektangelet er 120 cm

Oppgave 17

Formelen for figur n i et geometrisk mønster er Fn = 3n-2

a) Hva blir de tre første tallene i dette mønsteret?

b) Tegn de tre første figurene i dette mønsteret. Du kan selv velge om mønsteret skal bestå av kvadrater, sirkler, prikker eller andre former.

Oppgave 18

Utregningen under viser hvordan fire elever har regnet ut mattestykket: 6-3\cdot (5+5)-(-2^3)+3(-4)

Elev 1:

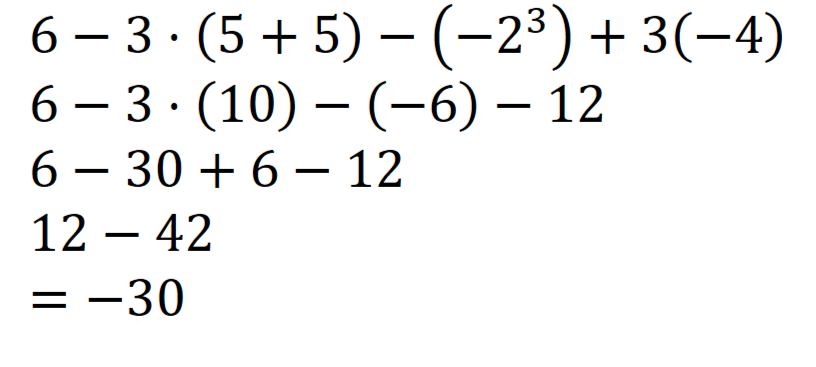
Elev 2:

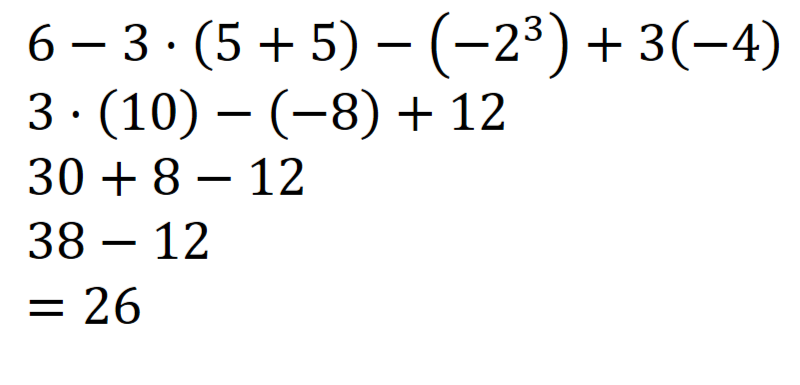
Elev 3:

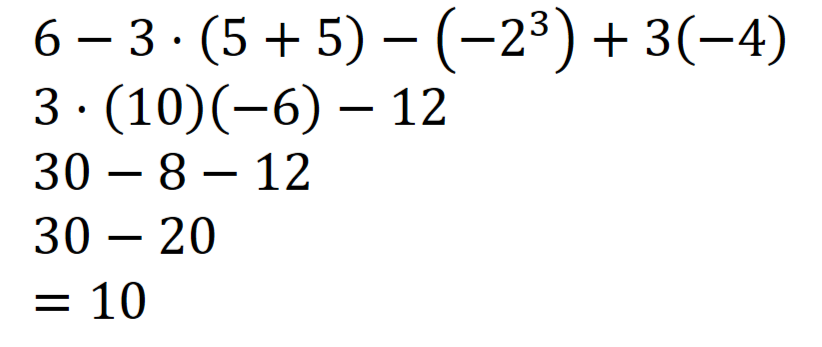
Elev 4:

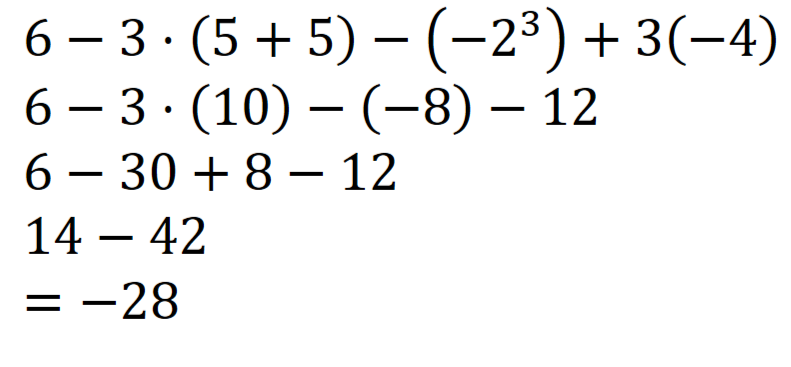
Forklar hvem av elevene som har regnet riktig, og hva som er feil hos de tre andre.

Oppgave 19

Under ser du hvordan Ove har regnet ut en likning:

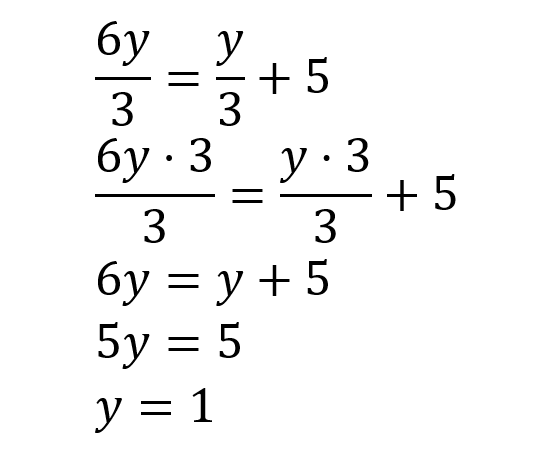
Argumenter for om framgangsmåten til Ove er riktig eller feil.

Oppgave 20

Oppstillingen under viser hva Petter og Alexander kjøper og betaler for noe fotballutstyr.

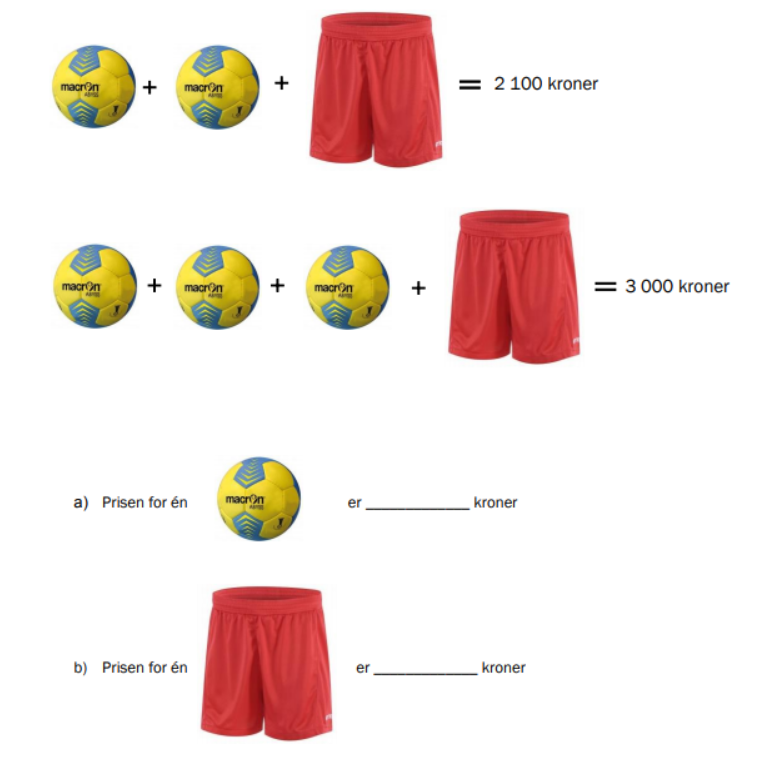
Oppgave 21

En vanntank inneholder 150 Liter vann. Når krana åpnes renner det ut 2,7 liter per minutt. Når det har gått x minutter, er det f(x) liter vann igjen på tanken. sammenhengen mellom f(x) og x kan uttrykkes som en funksjon slik:

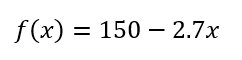
a) Framstill funksjonen grafisk i Geogebra.

b) Les av på y-aksen hvor mange liter det er igjen på tanken etter at kranen har vært åpen i 26 minutter(x-aksen).

c) Hvor lang tid tar det før tanken er tom for vann?

Oppgave 22

Koden under skriver ut verdien av uttrykket (u):  når a = 6 og b = 3

a) Forklar hvorfor programmet skriver ut svaret 33.

b) Lag en kode i Python som viser verdien av uttrykket: 2a+6b, når a = 7 og b = 2