Brøkregning er klassisk både på skriftlige og muntlige eksamener. Du skal kunne vise eller forklare hvordan du vil jobbe med de fire regneartene i forbindelse med brøk. Vi skal her se litt nærmere på hver av dem, men vi starter med en liten oppsummering:

  • Addisjon: For å plusse brøker, så må man ha felles nevner. Deretter legger man sammen telleren, og beholder fellesnevneren.
  • Subtraksjon: Ved minus gjelder de samme reglene som ved pluss
  • Multiplikasjon: Den enkle; teller ganger teller, og nevner ganger nevner
  • Divisjon: Vi starter med å snu den bakerste brøken, og deretter så multipliserer vi brøkene

Addisjon og subtraksjon av brøker

Når vi skal legge sammen eller trekke fra to brøker, så må vi ha samme nevner. Hvorfor? Vel, vi kan jo se på et lite eksempel:

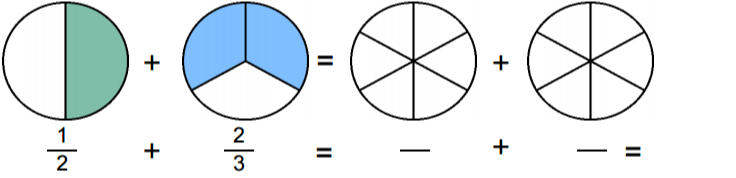
Her ser man på bildene at vi skal legge sammen en halv med to tredeler. Hvordan kan vi klare det? Det nærmeste jeg kommer, er at svaret må bli litt over en, siden to tredeler er litt mer enn en halv. Hvis du ser på bildet, så kan sirklene deles i flere små biter, og hvis vi deler dem inn i seks like store segmenter, så kan vi faktisk fargelegge både en halv og to tredeler. En halv vil bli 3 av 6 mens to tredeler vil bli 4 av 6. Derfor blir utregningen lik dette:

\frac{1}{2}+\frac{2}{3}=\frac{1\cdot 3}{2\cdot 3}+\frac{2\cdot 2}{3\cdot 2}=\frac{3}{6}+\frac{4}{6}=\frac{7}{6}

Som vi ser på mellomregningen, så har vi utvidet den første brøken med 3 og den andre brøkenhar vi utvidet med 2. Dette for at de skal ha samme (felles) nevner; nemlig 6.

Å utvide brøker er en metode som vi bruker for at brøkene skal få felles nevner, uten å endre verdien på brøken. Vi kan utvide brøker med hva vi vil, uten at verdien på brøken endres.

Hvordan finne felles nevner?

Her har jeg en helt grei metode som jeg benytter meg av hver gang. La oss ta et eksempel:

\frac{5}{6}-\frac{1}{8}=

Her skal jeg altså forholde meg til sjettedeler og åttedeler. Jeg finner fellesnevner ved å:

  • Kan jeg benytte meg av den største nevneren?
    • Nei, jeg kan ikke gange 6 med noe å få 8
  • Da ganger jeg den største nevneren med 2. Blir det en felles nevner?
    • Nei, Jeg kan ikke gange 6 med noe å få 16
  • Da ganger jeg den største nevneren med 3. Blir det en felles nevner?
    • Ja, jeg kan gange 6 med 4, og jeg vil få 24. Jeg har funnet en felles nevner

Dersom det ikke ville fungert med å gange med 3, så ville jeg prøvd 4 osv. Denne metoden vil alltid finne en fellesnevner, men det en sjelden gang så vil den finne en fellesnevner som er unødig stor, men dette gjør faktisk ingenting. Alt vil bli riktig allikevel. Så; nå har jeg funnet fellesnevner, hva gjør jeg nå? Vel, jeg må utvide begge brøkene slik at de får en lik nevner:

\frac{5}{6}-\frac{1}{8}=\frac{5\cdot 4}{6\cdot 4}-\frac{1\cdot 3}{8\cdot 3}=\frac{20}{24}-\frac{3}{24}=\frac{17}{24}

Jeg utvider brøkene, og når jeg har felles nevner så er oppgaven enkel!!!

Multiplikasjon av brøker

Multiplikasjon (ganging) av brøker er faktisk det enkleste. For å multiplisere to brøker trenger du bare å gange tellerene med hverandre får å få telleren i svaret, og nevnerene med hverandre for å få nevneren i svaret. Jeg kan vise med et lite eksempel:

\frac{5}{6}\cdot \frac{1}{8}=\frac{5\cdot 1}{6\cdot 8}=\frac{5}{48}

Vanskeligere enn det er det ikke!!!

Divisjon av brøk

Divisjon av brøk er ikke veldig mye vanskeligere enn multiplikasjon. Faktisk så er det helt likt, bare at vi må gjøre en liten ting først: snu den bakerste brøken. Snu? Ja, sånn at \frac{x}{y} blir til \frac{y}{x}. Ser du, telleren og nevneren har byttet plass. La oss ta et lite eksempel:

\frac{1}{4}:\frac{2}{7}=Jeg snur den bakerste brøken,
og bytter regneart til ganging…
\frac{1}{4}\cdot \frac{7}{2}=\frac{7}{8}…og jeg finner svaret ved å
gange brøkene med hverandre

Som du ser så er det faktisk bare ved pluss og minus at vi trenger fellesnevner. Ganging og deling er faktisk enklere.

Hvis du trenger noen oppgaver, så kan du vel bryne deg på disse!

\frac{1}{3}+\frac{3}{4}=\frac{4}{5}+\frac{1}{6}=\frac{3}{5}+\frac{1}{3}=
\frac{1}{3}-\frac{2}{7}=\frac{8}{5}-\frac{2}{3}=\frac{8}{9}-\frac{7}{12}=