Som om ikke det var nok med x’er i likninger, så skal vi nå begynne å blande inn y’er. Ta det med ro; det blir ikke dobbelt så vanskelig selv om det er dobbelt så mange variabler. Se på dette eksemplet:
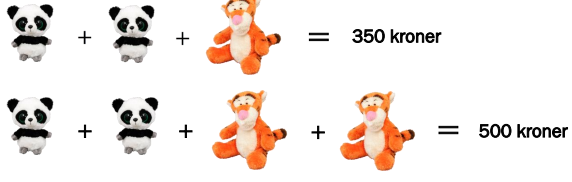
Dette er en flott oppgave som krever at elever ser etter en sammenheng, som de deretter må benytte seg av i en annen sammenheng. Måten jeg løser den på er som følger:
- 2 pandaer og 1 tiger koster 350 kr. Den informasjonen benytter jeg meg av i den andre linja også
- Den andre linja har en tiger ekstra, men den koster også 150 kr mer.
- Da koster den tigeren 150 kr
- Hvis tigeren i den første linja koster 150 kr, så koster de to pandaene 200 kr.
- Da koster en panda 100 kr
Da har vi klart å løse det praktiske problemet ved hjelp av litt praktisk logikk, og selv om dette ser ut som en typisk “Facebook-nøtt”, så er det faktisk en likningsoppgave i forkledning. Vi kan raskt oversette det praktiske problemet til et algebraisk problem. Dersom vi kaller en panda for x og en tiger for y, så får vi følgende:![]()
![]()
Ser du sammenhengen? Bra! Nå skal vi løse det algebraiske problemet på en algebraisk måte. Følg med, og forsøk å se sammenhengen med den logikken vi benyttet istad:
| Jeg ser at jeg har like mange av en variabel i begge likningene, nemlig 2x. Da tar jeg en likning og trekker fra den andre likningen. 2x-2x=0, 2y-y=y og 500-350=150 | |
| Da har jeg funnet y, og jeg setter den informasjonen inn i den øverste likningen. | |
| Jeg trekker fra 150 på begge sider | |
| Jeg deler på 2 på begge sider | |
| …og jeg har løst det algebraiske problemet. |
Se om du klarer å løse dette likningsettet med den samme logikken:
![]()
![]()
Hva er det som gjør at disse likningssettene lar seg løse såpass enkelt? Jo, det at begge likninger har like mange av en variabel. Da kan vi bare se på differansen av de andre leddene, også får vi en enkel likning med en ukjent! Da vet vi altså at dersom vi har like mange av en variabel i likningene, så klarer vi å komme oss videre. Hva gjør vi så hvis likningene ser sånn ut:![]()
![]()
Vel, vi kan ganske enkelt manipulere en likning, slik at vi får like mange variabler. Hvilken likning vi ønsker å bruke, spiller ingen rolle. Se på den øverste likningen. Dersom 2x og en y tilsvarer 22 så må dobbelt så mange variabeler tilsvare 44. Det betyr at 3 ganger så mange variabler tilsvarer 66. Det betyr at jeg kan gange hele den øverste likningen med 3, og jeg får da:![]()
![]()
Ser du? Nå har jeg like mange y’er i hver linje, og jeg kan begynne å lete etter en differanse. Jeg ser nå at 5x’er tilsvarer 35 osv…
Derom du hang med på dette, så kan du vel prøve deg på en liten oppgave også. Finn x og y i likningsettet under:
![]()
![]()
Hva gjør vi så hvis likningene er direkte uorganisert, sånn som i bildet i toppen av innlegget? Her er det viktig at vi ikke gjør dette mer komplisert enn det er. Vi vet hvordan vi kan behandle likninger for å omorganisere dem, og det gjør vi også her:
| Dette likner ikke på noen oppgaver vi har sett på tidligere. Slapp av, pust med magen. Vi omorganiserer den øveste likningen! Jeg vil ha variabler på venstre side, og konstanter på høyre side. Jeg bruker den øverste likningen og trekker fra 4x på begge sider. | |
| Deretter må jeg omorganisere likningen. 2y-4x blir til -4x+2y | |
| Hvis jeg skal få like mange av en variabel så multipliserer jeg den nederste likningen med 2. | |
| Nå ser jeg på differansen av likningene. Den nederste likningen har 6x’er mer (forskjellen på 2 og -4), og en verdi som er 12 mer (forskjellen på 6 og -6). | |
| Hvis jeg vet hva 6 x’er er, så deler jeg på 6 på begge sider. | |
| …og denne informasjonen kan jeg sette inn i en av de to opprinnelige likningene. Jeg velger den nederste, for den ser enklest ut. | |
| Trekker fra 2 på begge sider… | |
| Sånn! |
Det gikk an å henge med på dette, vel? Hvis ikke, prøv å gå gjennom en gang til, eller vent til mattetimen og spør meg da! 🙂
Hvis du hang med, så skal du få noen oppgaver og bryne deg på:
| Oppgave 1 |
| Oppgave 2 |
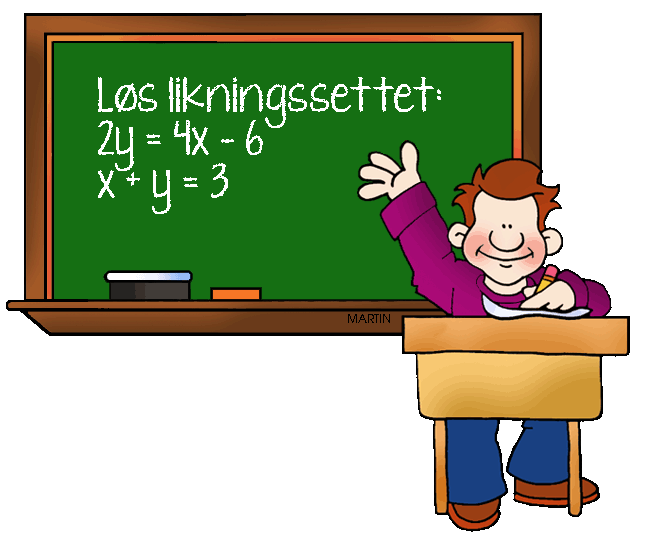
Recent Comments